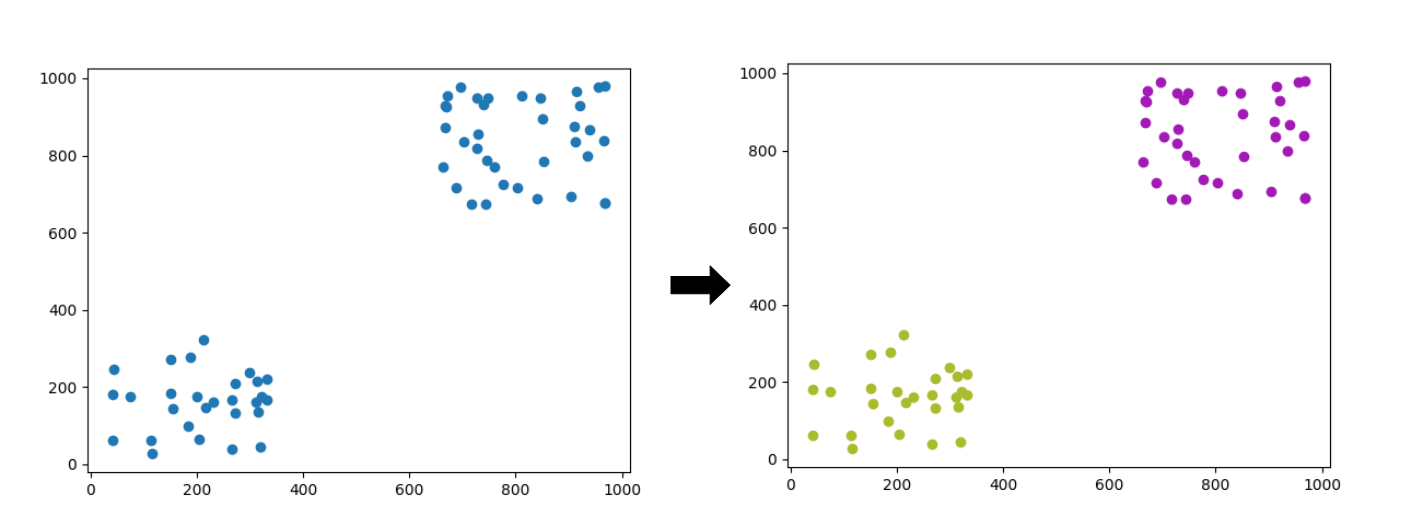
k means clustering divides arbitrary data k clusters based on their similarity (or distance). This algorithm is effective at grouping unclustered data if you cannot have access to artificial intelligence, but the result is not uniform due to randomness and it may require long time to compute the results.
However, the result will be acceptable as long as the data pattern is well-categorized and the algorithm is easy to understand and implement.
1. How Does it Work?
First of all, the data need to be able to produce similarities between them, such as in forms of distance. One example is a vector of (1 x N). Given two vectors, their distance can be calculated with Manhattan distance or Euclidean distance. A 2D coordinates is also a vector, with the shape of (1 x 2).
They can be referred to as L1 distance and L2 distance repectively. If you want to give more weights on bigger differences, choose L2 (Euclidean) distance since the bigger the difference is, the much bigger the squared result is. Otherwise, choose L1 (Manhattan) distance.
To describe keypoints, k means algorithms works as below:
- Select initial centroids randomly.
- Map each vector to the nearest centroid.
- Calculate the next centroids by averaging the vectors within a cluster.
- Repeat 2-3 until no changes further.
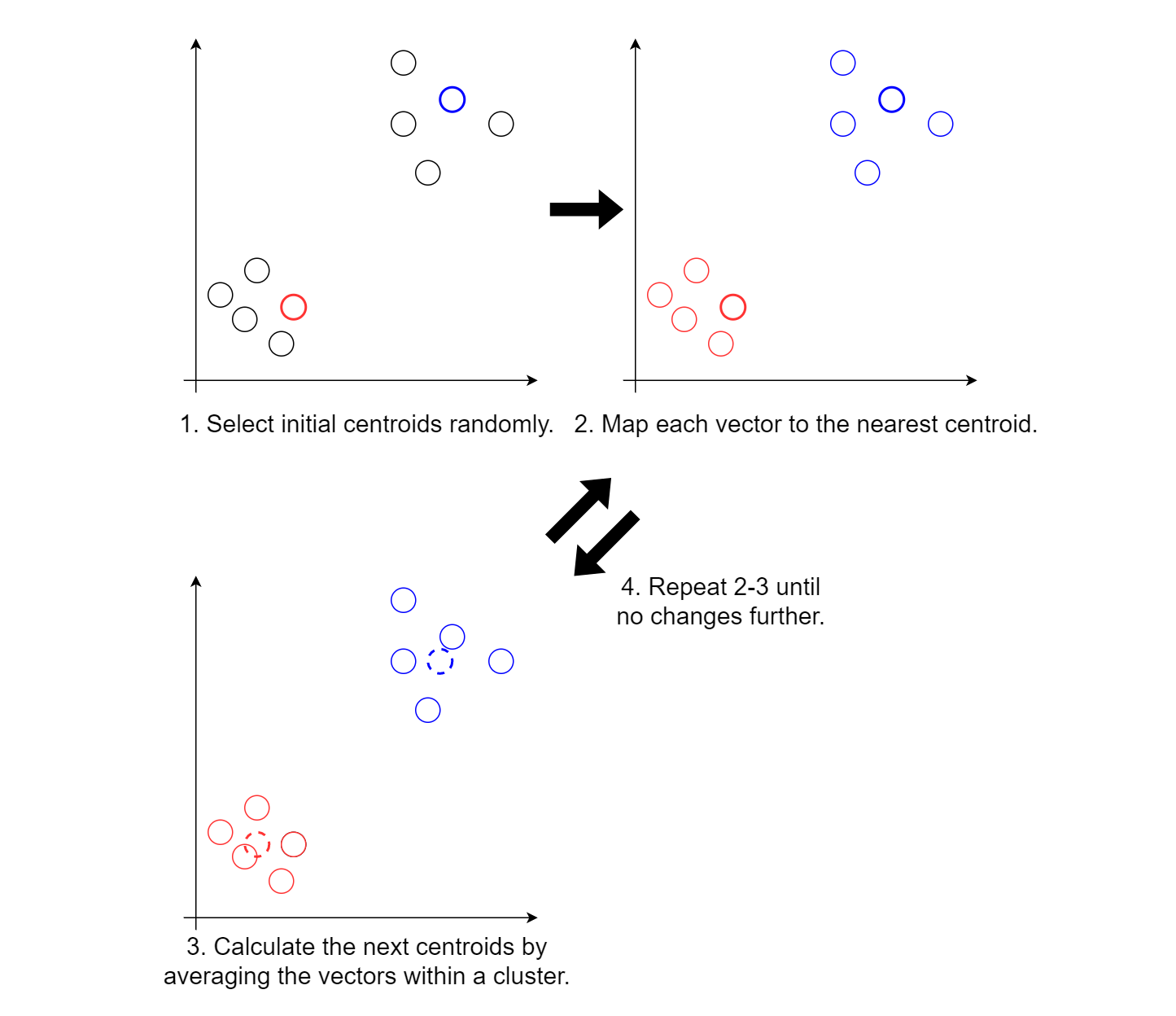
1) Select Initial Centroids Randomly.
Since we have no information on the data, we randomly select k vectors and call them centroids. We are skipping how to select them better, but it will be much more effective to select vectors that can well-represent each cluster. Why don't you try to select vectors as much far from each other as you can within reasonable time?
2) Map each Vector to the Nearest Centroid.
For each vector, find the nearest centroid and group them together (cluster). It may not look fine with random initial centroids, but it is okay. We will find better centroids fron now on.
3) Calculate the next Centroids by Averaging the Vectors within a Cluster.
For each cluster you acquired, get the average of vectors that reside in the cluster. The output will represent the vectors in the cluster. You might have noticed that the outputs show the clusters better than the previous clusters do. Replace the centroids with the average vectors.
4) Repeat 2-3 until no Changes further.
Repeat step 2 and 3 until centroids converge. It may take long if the initial centroids are not well-chosen or there are too many data so computing the next centroids is hard work. In that case, you may decide to exit the loop after some N repetition or the differences between the previous and the next centroids are negligible.
2. k Means Clustering in Python Code
def kmeans_cluster(k:int, vectors:List[List[float]])->List[List[List[float]]]:
''' Run k means clustering on given vectors and return centroids.
k must be equal or smaller than the number of vectors.
'''
num_vectors=len(vectors)
vector_len=len(vectors[0])
assert k<=num_vectors
# Select initial centroids randomly.
indices=random.sample(range(num_vectors), k)
centroids=[vectors[index] for index in indices]
# This list stores nearest centroid of each row.
nearest_centroid=[0]*num_vectors
The method gets two parameters, k and vectors. vectors parameters is
of type of List[List[float]], such as [[1, 2], [10, 13], [3, 4]].
The assert statement ensures k is equal to the number of vectors or larger. It does not necessarily have to satisfy the condition, but in that case there will be no meaning.
As we discussed eariler, we need to pull some
# Repeat run until converging.
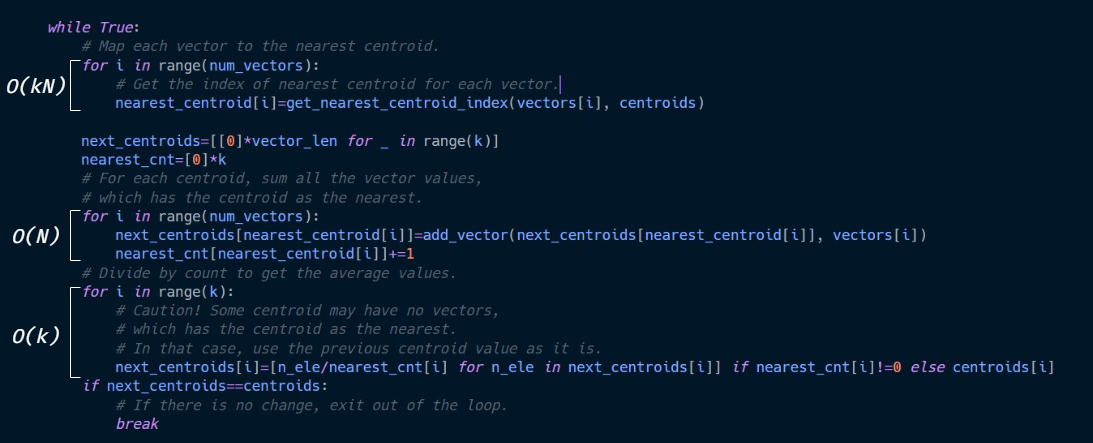
while True:
# Map each vector to the nearest centroid.
for i in range(num_vectors):
# Get the index of nearest centroid for each vector.
nearest_centroid[i]=get_nearest_centroid_index(vectors[i], centroids)
next_centroids=[[0]*vector_len for _ in range(k)]
nearest_cnt=[0]*k
# For each centroid, sum all the vector values,
# which has the centroid as the nearest.
for i in range(num_vectors):
next_centroids[nearest_centroid[i]]=add_vector(next_centroids[nearest_centroid[i]], vectors[i])
nearest_cnt[nearest_centroid[i]]+=1
# Divide by count to get the average values.
for i in range(k):
# Caution! Some centroid may have no vectors,
# which has the centroid as the nearest.
# In that case, use the previous centroid value as it is.
next_centroids[i]=[n_ele/nearest_cnt[i] for n_ele in next_centroids[i]] if nearest_cnt[i]!=0 else centroids[i]
Within the while loop, we map each vector with the nearest centroid.
After that, we get the average of vectors within each cluster,
by summing all the vectors and dividing by the number of vectors.
In cases where there is no vector within a cluster (It sounds not
possible, but it does happen sometimes!),
we keep the previous centroid value.
if next_centroids==centroids:
# If there is no change, exit out of the loop.
break
centroids=next_centroids
# Cluster vectors with the calculated centroids.
clusters=cluster_vectors(vectors, centroids)
return clusters
If the next centroids are equal to the previous, congrats, we finally converge! Exit the loop, and cluster data with the converged centroids and return. Else, re-run the process until converge is made.
3. Hierarchical k Means Clustering
k means clustering algorithm is great, but it has serious
problem: the computational time.
Let us say the number of vectors is N.
Then the time complexity of the loop is:
... Therefore
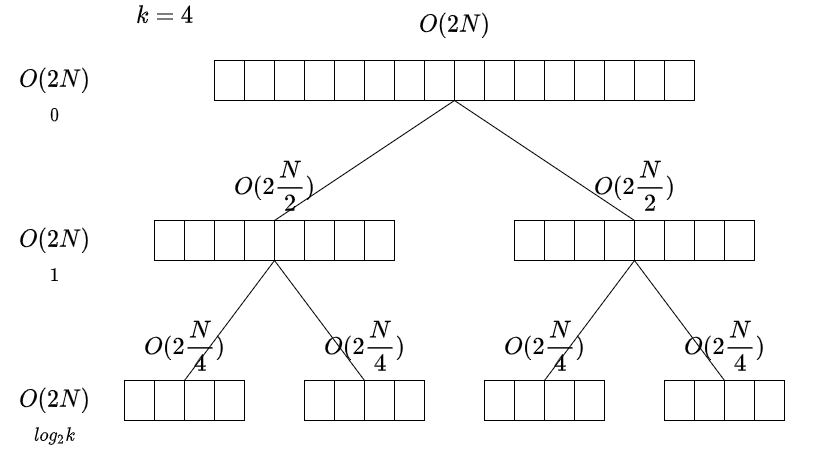
This is the point where hierarchical k means clustering rolls.
The algorithm divides data into 2 clusters (or more but 2
most of the time), recursively calls itself on each clustered data.
Think of a binary tree. Or some algorithm like merge sort.
By recursively calling itself, the algorithm sub-divides the cluster,
creating another 2 sub-clusters from one cluster. The time complexity
is
On my PC environments, with
4. Hierarchical k means Clustering in Python Code
def hierarchical_kmeans_cluster(k:int, vectors:List[List[float]])->List[List[List[float]]]:
''' Run k-means clustering on given vectors hierarchically and return.
k must be equal or smaller than the number of vectors.
Also k has to be an integer having value 2^n.
'''
num_vectors=len(vectors)
assert k<=num_vectors
# Check if k is 2^n.
assert k>0 and (k & (k-1))==0
# Run k means clustering with k=2.
clusters=kmeans_cluster(2, vectors)
if k//2==1:
# Stop calling recursively and return.
return clusters
# Divide vectors into two groups by the nearest centroid.
clusters_0=hierarchical_kmeans_cluster(k//2, clusters[0])
clusters_1=hierarchical_kmeans_cluster(k//2, clusters[1])
return [*clusters_0, *clusters_1]
Implementation of hierarchical k means clustering is simple.
Divide the vectors into two clusters using kmeans_cluster
we have implemented. If we do not need to sub-divide clusters
by checking if k//2==1, return the clusters as they are.
Otherwise recursively call hierarchical k means clustering on
each clusters with